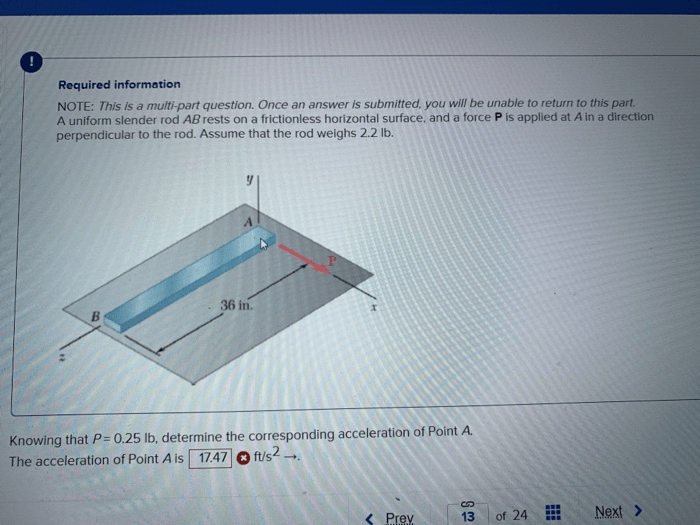
A uniform rigid rod rests on a level frictionless surface – A uniform rigid rod resting on a level frictionless surface presents a captivating study in mechanics, offering insights into the fundamental principles governing static equilibrium and rotational motion. This analysis delves into the forces acting on the rod, its moment of inertia, and the intricate relationship between its angular velocity and acceleration.
By examining the interplay of these concepts, we gain a deeper understanding of the rod’s behavior and its practical applications in various real-world devices.
Uniform Rigid Rod on a Frictionless Surface

A uniform rigid rod is a rod with a uniform cross-section and density throughout its length. When placed on a level frictionless surface, it can rotate freely about an axis perpendicular to the surface and passing through its center of mass.
Static Equilibrium
Static equilibrium occurs when the net force and net torque acting on an object are both zero. In the case of a uniform rigid rod resting on a frictionless surface, the forces acting on the rod are its weight, acting downwards through its center of mass, and the normal force, acting upwards through the point of contact with the surface.
Since the rod is in equilibrium, the net force and net torque must be zero. This means that the weight of the rod must be equal to the normal force, and the torque due to the weight must be equal to the torque due to the normal force.
Moment of Inertia
The moment of inertia of a rigid body is a measure of its resistance to rotational motion. For a uniform rigid rod rotating about an axis perpendicular to its length and passing through its center of mass, the moment of inertia is given by:
$$I = \frac112 m L^2$$
where mis the mass of the rod and Lis its length.
The moment of inertia is an important quantity because it determines the rod’s rotational motion. A rod with a large moment of inertia will be more difficult to rotate than a rod with a small moment of inertia.
Rotational Motion, A uniform rigid rod rests on a level frictionless surface
When a uniform rigid rod is subjected to a torque, it will rotate about an axis perpendicular to the torque. The angular acceleration of the rod is given by:
$$ \alpha = \frac\tauI $$
where αis the angular acceleration, τis the torque, and Iis the moment of inertia.
The angular acceleration is directly proportional to the torque and inversely proportional to the moment of inertia. This means that a rod with a large moment of inertia will have a smaller angular acceleration than a rod with a small moment of inertia.
Applications
Uniform rigid rods are used in a variety of applications, including:
- Pendulums: A pendulum is a weight suspended from a pivot point by a rod. The rod is a uniform rigid rod, and the pendulum’s period of oscillation is determined by the rod’s length and moment of inertia.
- See-saws: A see-saw is a rigid rod supported by a pivot point in the middle. Children can play on a see-saw by pushing on the ends of the rod. The rod’s moment of inertia determines how easily the see-saw can be tipped.
- Levers: A lever is a rigid rod that is used to lift or move objects. The rod’s moment of inertia determines how much force is required to lift or move the object.
Expert Answers: A Uniform Rigid Rod Rests On A Level Frictionless Surface
What is the significance of the moment of inertia in rotational motion?
The moment of inertia quantifies an object’s resistance to angular acceleration. A higher moment of inertia indicates greater resistance, making it more difficult to change the object’s rotational motion.
How does the absence of friction affect the motion of the rod?
Friction is a force that opposes motion between two surfaces in contact. Its absence in this scenario eliminates any hindrance to the rod’s movement, allowing it to rotate freely without energy loss due to friction.